PRUEBA DE HIPOTESIS PARA LA MEDIA, VARIANZA Y PROPORCION

PRUEBA DE HIPÓTESIS PARA LA MEDIA.

En vez de estimar el valor de un parámetro, a veces se debe decidir si una afirmación relativa a un parámetro es verdadera o falsa. Es decir, probar una hipótesis relativa a un parámetro. Se realiza una prueba de hipótesis cuando se desea probar una afirmación realizada acerca de un parámetro o parámetros de una población.

Una hipótesis es un enunciado acerca del valor de un parámetro (media, proporción, etc.).

Prueba de Hipótesis es un procedimiento basado en evidencia muestral (estadístico) y en la teoría de probabilidad (distribución muestral del estadístico) para determinar si una hipótesis es razonable y no debe rechazarse, o si es irrazonable y debe ser rechazada.

La hipótesis de que el parámetro de la población es igual a un valor determinado se conoce como hipótesis nula. Una hipótesis nula es siempre una de status quo o de no diferencia.

En toda prueba de hipótesis se presentan 3 casos de zonas críticas o llamadas también zonas de rechazo de la hipótesis nula, estos casos son los siguientes:

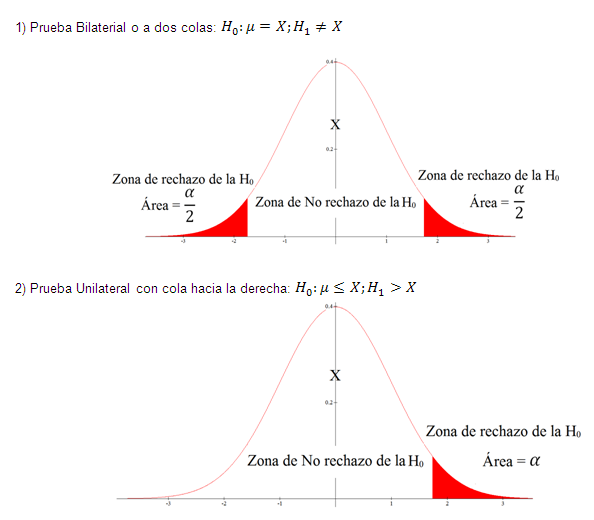
En toda prueba de hipótesis se pueden cometer 2 tipos de errores:

Prueba medias de una muestra

Se utiliza una prueba de una muestra para probar una afirmación con respecto a una media de una población única.

Nota: Se considera práctico utilizar la distribución t solamente cuando se requiera que el tamaño de la muestra sea menor de 30, ya que para muestras más grandes los valores t y z son aproximadamente iguales, y es posible emplear la distribución normal en lugar de la distribución t.

PRUEBA DE HIPÓTESIS DE LA VARIANZA

Pruebas de hipótesis para una varianza Es un procedimiento para juzgar si una propiedad que se supone cumple una población estadística es compatible con lo observado en una muestra de dicha población en este caso la varianza, para ello formularemos dos Hipótesis (llamada "Hipótesis Nula") y (llamada "Hipótesis Alternativa"), con ellas realizaremos una o mas pruebas, para tratar de encontrar cual deberíamos rechazar. En este procedimiento lo que buscamos es, mediante unos criterios de rechazo preestablecidos, tratar de desmentir nuestra “Hipótesis Nula” por lo cual tomaríamos la “Hipótesis alternativa”, de lo contrario no rechazaríamos nuestra ”Hipótesis Nula” y desecharíamos la ”Hipótesis 

la función Chi cuadrado tiene una distribución de datos de la siguiente forma:

Lo que nos da a entender que a diferencia de las distribuciones normales y t Student que hemos venido trabajando, Chi cuadrado no es simétrica, es por esto que cuando hallamos los limites para una prueba de hipótesis a dos colas, debemos hallar el chi cuadrado de y ,a diferencia de las otras dos distribuciones mencionadas anteriormente, en las cuales solo era necesario calcular uno de estos valores y el otro limite se conocería multiplicando el hallado por 1. A continuación enseñaremos a manejar la tabla de la distribución Chi cuadrado. En esta nos dan dos parámetros, el primero es en el que nos relaciona con , y el segundo que representa los grados de libertad, para efectos prácticos, en la tabla se busca de la siguiente forma:

Siendo A el relacionado con, y b los grados de libertad.

PRUEBA DE HIPÓTESIS DE LA PROPORCIÓN

Las pruebas de proporciones son adecuadas cuando los datos que se están analizando constan de cuentas o frecuencias de elementos de dos o más clases. El objetivo de estas pruebas es evaluar las afirmaciones con respecto a una proporción (o Porcentaje) de población. Las pruebas se basan en la premisa de que una proporción muestral (es decir, x ocurrencias en n observaciones, o x/n) será igual a la proporción verdadera de la población si se toman márgenes o tolerancias para la variabilidad muestral. Las pruebas suelen enfocarse en la diferencia entre un número esperado de ocurrencias, suponiendo que una afirmación es verdadera, y el número observado realmente. La diferencia se compara con la variabilidad prescrita mediante una distribución de muestreo que tiene como base el supuesto de que  es realmente verdadera.

En muchos aspectos, las pruebas de proporciones se parecen a las pruebas de medias, excepto que, en el caso de las primeras, los datos muestrales se consideran como cuentas en lugar de como mediciones. Por ejemplo, las pruebas para medias y proporciones se pueden utilizar para evaluar afirmaciones con respecto a:

1) Un parámetro de población único (prueba de una muestra)

2) La igualdad de parámetros de dos poblaciones (prueba de dos muestras), y

3) La igualdad de parámetros de más de dos poblaciones (prueba de k muestras). Además, para tamaños grandes de muestras, la distribución de muestreo adecuada para pruebas de proporciones de una y dos muestras es aproximadamente normal, justo como sucede en el caso de pruebas de medias de una y dos muestras.

Prueba de proporciones de una muestra

Cuando el objetivo del muestreo es evaluar la validez de una afirmación con respecto a la proporción de una población, es adecuado utilizar una prueba de una muestra. La metodología de prueba depende de si el número de observaciones de la muestra es grande o pequeño.

Como se habrá observado anteriormente, las pruebas de grandes muestras de medias y proporciones son bastante semejantes. De este modo, los valoresestadísticos de prueba miden la desviación de un valor estadístico de muestra a partir de un valor propuesto. Y ambas pruebas se basan en la distribución normal estándar para valores críticos. Quizá la única diferencia real entre las ambas radica en la forma corno se obtiene la desviación estándar de la distribución de muestreo.

Esta prueba comprende el cálculo del valor estadístico de prueba Z

Posteriormente este valor es comparado con el valor de Z, obtenido a partir de una tabla normal a un nivel de significación seleccionado.

Como ocurrió con la prueba de medias de una muestra, las pruebas de proporciones pueden ser de una o dos colas.

La primera alternativa establece una prueba de cola derecha, la segunda, izquierda y la tercera, una prueba de dos colas.

Ejemplo ilustrativo

En un estudio se afirma que 3 de 10 estudiantes universitarios trabajan. Pruebe esta aseveración, a un nivel de significación de 0,025, respecto a la alternativa de que la proporción real de los estudiantes universitarios trabajan es mayor de lo que se afirma, si una muestra aleatoria de 600 estudiantes universitarios revela que 200 de ellos trabajan. La muestra fue tomada de 10000 estudiantes.

Los datos son:

Como en los datos aparece el tamaño de la población, se debe verificar si el tamaño de la nuestra es mayor que el 5%. Se remplaza valores en la siguiente fórmula: